Reconfigurable Hinged Kirigami Tessellations

ETH Zurich, Interactive Geometry Lab (IGL)

SIGGRAPH Asia 2025

We introduce a computational method for designing kirigami patterns that reconfigure flat sheets into complex shapes. By analyzing planar tilings and their rotational deployment, we identify valid cuts and generate novel, physically realizable structures. This enables inverse design of expressive, gap-free geometries through combinatorial reconfiguration.

Background

Definition 1 (complete cut of a planar tiling)

For a planar tiling (i.e., a 2D manifold polygonal mesh with disk topology contains no holes), we call a set of directed edges that covers all interior edges a complete cut. The direction of each cut determines how the neighboring faces hinge after cutting: cutting along it breaks their adjacency while preserving a hinge at the source vertex, producing a duplicate at the target vertex.

Note: The left image shows an example of a complete cut (black arrows). After making these cuts, the tiling can be transformed into a hinged kirigami structure example shown below.

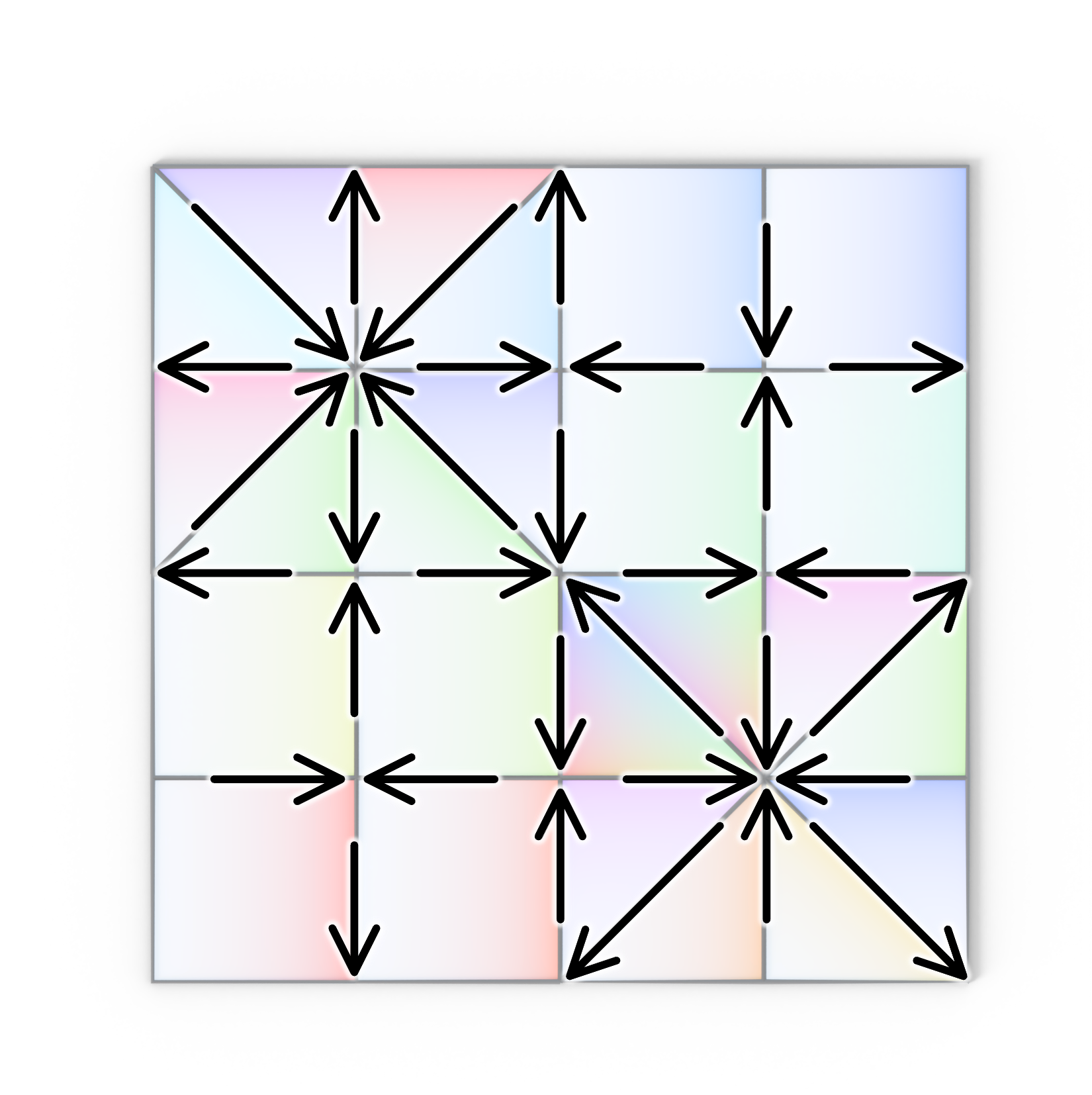
Definition 2 (hinged kirigami pattern & deployability)

We call a non-manifold mesh a hinged kirigami pattern if each interior vertex is incident to exactly two faces. A hinged kirigami pattern is deployable if its faces can rotate rigidly around hinge vertices without collision with neighboring faces. We call a tiling deployable if there exists a complete cut that transforms it into a deployable hinged kirigami pattern. We call the angle between the duplicated edges after cutting the opening angle. We call a deployable tiling uniformly deployable if the opening angles of all interior edges have the same value across all deployment configurations.

Note: the example on the left is uniformly deployable; its deployment is a one-parameter family of configurations parameterized by a single opening angle.

Core challenges

How can we determine whether a tiling is deployable, i.e., whether there exists a complete cut that transforms the tiling into a hinged kirigami structure whose faces can rotate rigidly about hinge vertices without collision?

Remark (combinatorial condition)

A planar manifold tiling can be cut into a valid hinged kirigami pattern if and only if all its interior vertices have even valency.

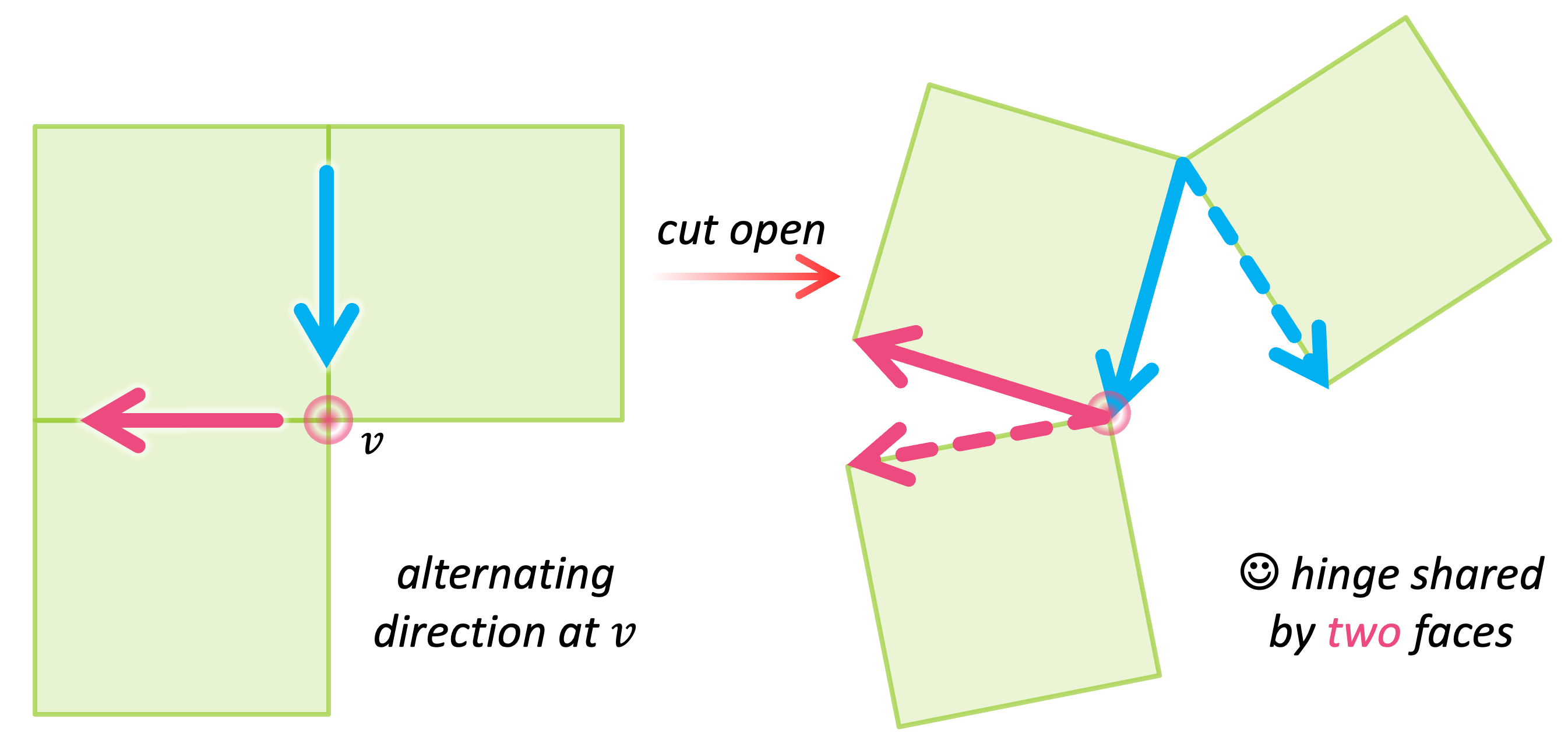
Note: to see why, consider the two adjacent cuts, they must have alternating directions to ensure that the hinge vertex after cutting is shared by exactly two faces. Please see Appendix A of our paper for the full proof.

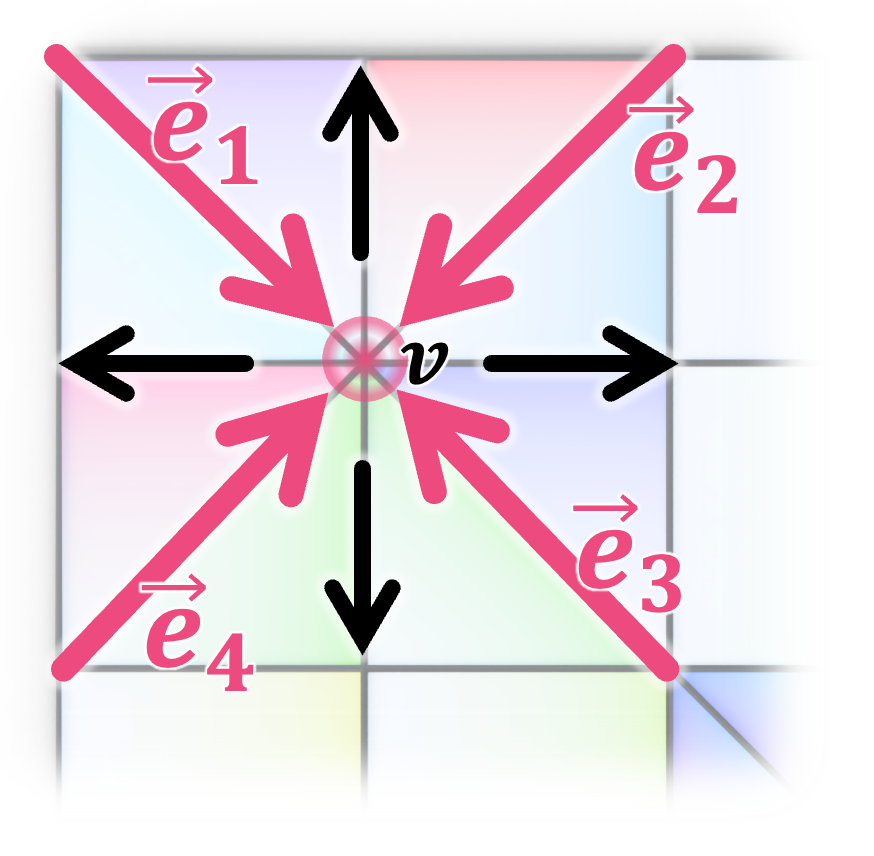
Definition 3 (deployment-friendly vertex)

Let \(\mathcal{T} = (\mathcal{V}, \mathcal{F})\) be a planar tiling with a complete cut \(\mathcal{E}_c\). Let \(v \in \mathcal{V}\) be a vertex of even valency \(2k\). Denote by \(\vec{e}_1, \cdots, \vec{e}_k\) the directed edges (cuts) in \(\mathcal{E}_c\) ending at \(v\), ordered cyclically. Vertex \(v\) is said to be deployment-friendly if \(\sum_{i=1}^k \vec{e}_i = \vec{0}\).

Note: the example on the left highlights a deployment-friendly vertex \(v\) with valency 8. The directed edges (cuts) ending at \(v\) are shown as arrows colored in red, and their vector sum equals \(\vec{0}\), satisfying the deployment-friendly condition.

Proposition (necessary and sufficient condition for uniform deployability)

For a planar tiling with all interior vertices of even valency, the following are equivalent: (1) Every interior vertex in the tiling is deployment-friendly. (2) The resulting hinged kirigami structure is uniformly deployable in 2D.

Note: the proof is based on the assumption of rigid face rotation and planar deployment, so the holes between faces remain planar during deployment. Please see Appendix B of our paper for the full proof.

Given a uniformly deployable hinged kirigami pattern, how can we mathematically characterize the bounds of face rotations about hinges, i.e., its opening angles, that define its maximally open configurations during deployment?

Remark

A deployable hinged kirigami pattern typically admits two distinct maximally open configurations during deployment: (1) maximal area expansion, where the pattern achieves its largest projected coverage area, and (2) maximal rotation angle, beyond which further rotation would cause face collisions.

For a uniformly deployable hinged kirigami pattern, its deployment can be parameterized by a single opening angle \(\theta\):

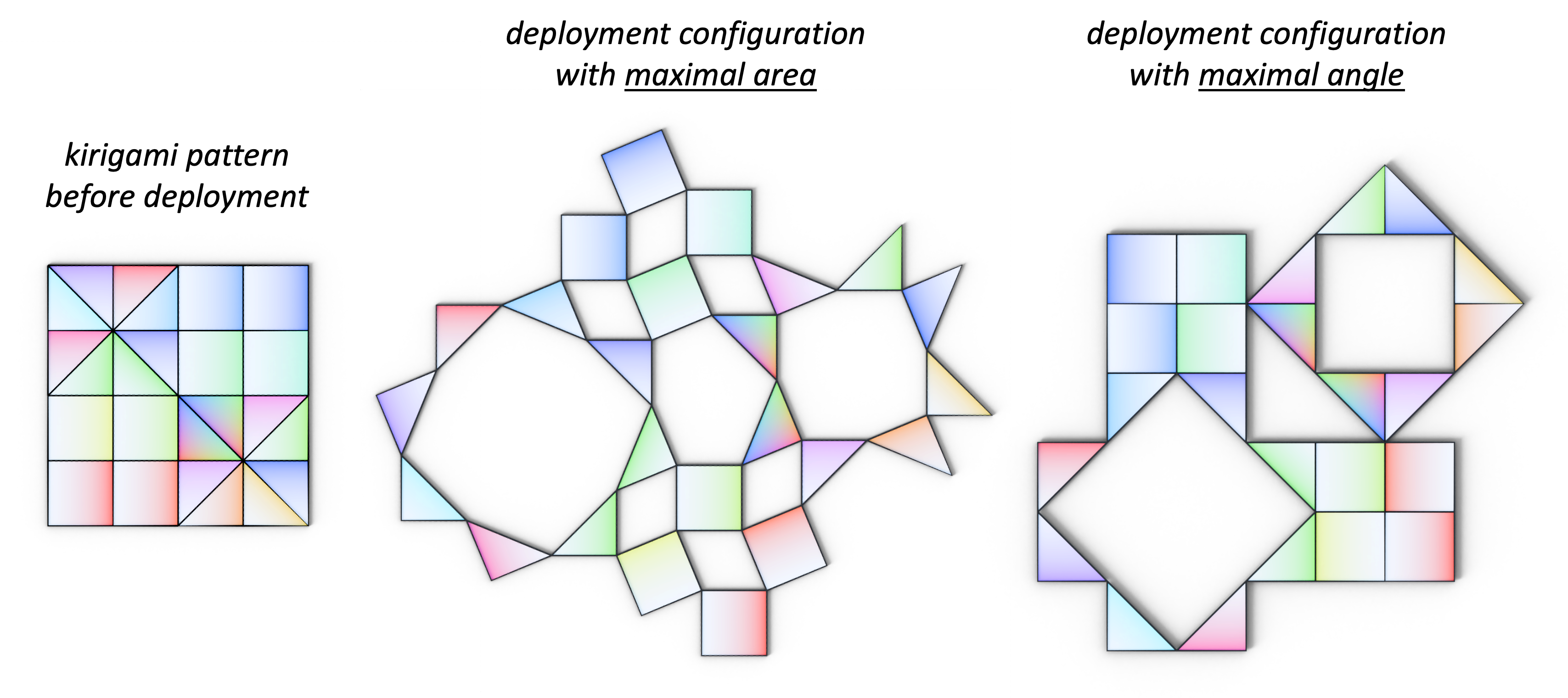
maximal area expansion configuration can be obtained by optimizing \(\theta\) to maximize the area of the open kirigami pattern, accounting both for faces in the tiling and holes induced by cuts.
maximal rotation angle configuration can be mathematically derived without optimization. Consider a hinge vertex \(v\) shared by two faces \(f_i\) and \(f_j\). Let \(\alpha_i\) and \(\alpha_j\) denote the internal angles at \(v\) for these two faces. The maximum opening angle allowed at \(v\) is \( 2\pi - \alpha_i - \alpha_j \). Rotating beyond this limit causes the faces to collide from the backside. Hence, the global maximum opening angle for the entire tiling is the minimum of these local vertex bounds; beyond this threshold, collisions are inevitable.

Note that maximal area expansion configuration is commonly used in prior works. In this work, we focus on maximal angle configuration as it offers the following advantages:

It can be derived explicitly without optimization, whereas the maximal area configuration for unconventional patterns often requires optimization
It provides intuitive fabrication instructions for deployment: rotate faces around hinges until they collide from the backside, rather than targeting specific angles
It enables a new approach for programmable curvature to emerge from local combinatorial changes without holes (see examples below)

How can we design 2D manifold tilings that are guaranteed to be deployable?

To generate a deployable tiling, we just need to make sure that all its interior vertices have even valency and are deployment-friendly.

Design Canvas

Click point A for group 1

Preview Canvas

deployment-unfriendly vtx will be highlighted

create tiling

grid size 40

grid type

kirigami pattern

\(n_x\)

\(n_y\)

auto play

angle 0°

deployment

ini max area max angle

export patterns

How can we computationally modify a 2D manifold tiling such that, when cut and rotated to the maximal opening angle, it achieves a desired 3D geometry?

Algorithm Overview

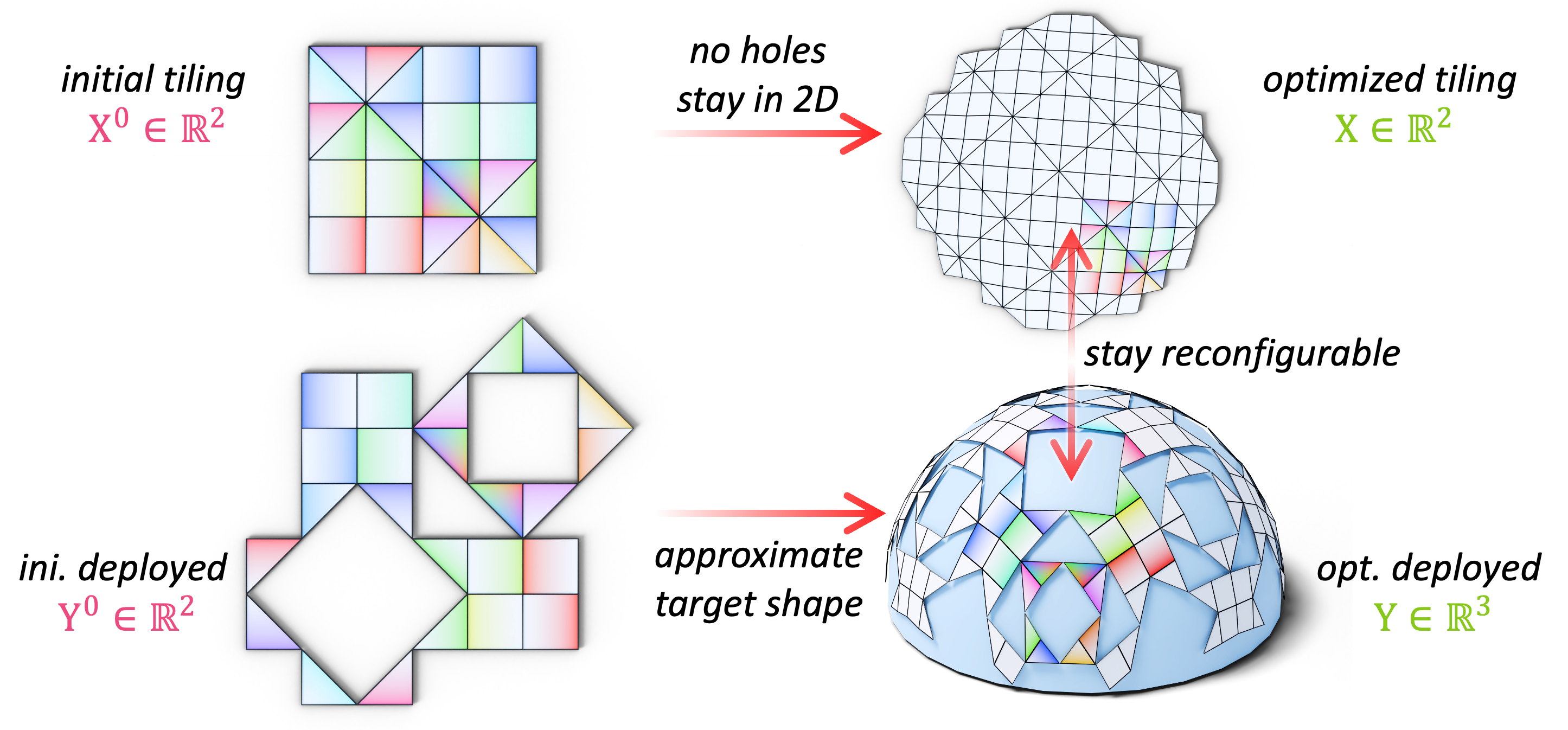
input: a specified tiling pattern and 3D target shape
output: optimized tiling with its
- 2D embedding \(\mathbf{X}\) before deployment
- 3D embedding \(\mathbf{Y}\) after deployment
objectives:
- planarity: deployed faces (\(\mathbf{Y}\)) are planar
- reconfigurability: corresponding faces before and after deployment stay rigid
- shape approximation: 3D embedding after deployment well approximates the target geometry
- fairness: the optimized tiling does not deviate too much from its initial shape
initializations:

\(\mathbf{X}\) is initialized by \(\mathbf{X}^0\), which is given as input
\(\mathbf{Y}^0\) is the deployed state of \(\mathbf{X}^0\), solved in Problem 2
we parameterize the target geometry into 2D and get the flattening function \(f\). We then use \(f^{-1}\) to lift up \(\mathbf{Y}^0\), i.e., \(\mathbf{Y}^1 = f^{-1}(\mathbf{Y}^0)\in\mathbf{R}^3\) get the initial guess of \(\mathbf{Y}\)

Note: please see Sec.4.3 and Appendix E of our paper for more details about the optimization objectives and implementation. The source code can be find at here.

Try it out :)

Load Target Mesh

No mesh loaded

Load Kirigami Pattern

Optimization

Parameters for initialization

scale

rot (°)

Weights for optimization

\(w_p\)

\(w_s\)

\(w_r\)

\(w_f\)

Errors

max avg

rigidityN/A

planarityN/A

shapeN/A

Initial Configuration

Deployed Configuration

Deployed configuration visualization